P-NP: ant sveiko proto svarstyklių
Indų kilmės Vinay Deolalikaras, dirbantis Hewlett-Packard laboratorijose Kalifornijoje (JAV), 2010 m. teigė, kad išsprendė P ir NP klasių tapatumo problemą, kuri yra viena 7-ių Tūkstantmečio problemų, už kurių išsprendimą Clay matematikos institutas skyrė po milijoną dolerių. Iš jų kol kas išspręsta tik viena Puankarė teiginys iš topologijos srities, kurį įrodė Grigorijus Perelmanas (beje, atsisakęs premijos).
 P ir NP klasių tapatumo klausimas yra vienas svarbiausių kompiuterijos moksle.
Jis labai svarbus kriptografijai, kuri iki šiol remiasi neįrodytomis prielaidomis, kurių viena yra kad P¹NP.
P ir NP klasių tapatumo klausimas yra vienas svarbiausių kompiuterijos moksle.
Jis labai svarbus kriptografijai, kuri iki šiol remiasi neįrodytomis prielaidomis, kurių viena yra kad P¹NP.
Vinay Deolalikaras savo įrodymą pateikė išsamiu rankraščiu, kurį galima perskaityti čia. Anot jo įrodinėjimo, P ir NP klasės nėra lygios. Jei įrodymas teisingas, tai reikštų, kad uždavinio sprendinio teisingumo nustatymas nėra tas pat kaip to sprendinio suradimas.
Visada yra vienas būdas, kaip kompiuteris gali išspręsti uždavinį tiesiog išbandydamas visas įmanomas kombinacijas. Tačiau, pavyzdžiui, jei bandote nulaužti užšifruotą informaciją, tai gali trukti nepaprastai ilgai. P ir NP problemos klausimo esmė ar galima automatizuoti kūrybiškumą? Vinay Deolalikaras įrodymas teigtų, kad negalima.
Kaip pagrindinį pavyzdį ir idėją, Deolalikaro įrodyme panaudojamas bulinio užtikrintumo uždavinys (k-SAT). Šio tipo uždaviniai nagrinėja loginę išraišką, susidedančią tik iš ir, arba bei ne operatorių, kintamųjų ir skliaustų, bandant nustatyti, ar gali kintamieji įgauti tokias taip ir ne reikšmes, kad išraiškos reikšmė būtų taip.
Įrodymas bando k-SAT uždavinį perteikti kaip užklausas grafinėse struktūrose. Panaudojama geometrinė FO (LPF) logikos interpretacija, užgriebianti visas per polinominį laiką paskaičiuojamas užklausas. Jei k reikšmė yra pakankamai didelė, tada sprendinio erdvė tampa milžiniška ir eksponentinis sprendinių skaičius bus generuojamas per LFP konstrukciją. Tai aiškiai parodo, kad LPF negali išreikšti užtikrintumo užklausos ... ir atskiria P nuo NP.
1971-aisiais Stephen Cook'as*), jaunas Toronto un-to profesorius dar neapsiplunksnavęs kompiuterių mokslo srityje iškėlė šį klausimą. Nuo tada buvo pateikta vos saujelė galimų sprendimų, kurių visi greitai buvo paneigti. Tad S. Kukas labai džiaugiasi Vinay Deolalikaro bandymu. Tačiau gilinantis į jo įrodinėjimą, galvą ėmė kaišioti trūkumai. Vinay Deolalikaras pateikė pataisytą įrodymo versiją, tačiau išliko nepataisomos konceptualaus lygio problemos.
Matematikai įtaria, kad Vinay Deolalikaro įrodymas gali nepraeiti labai paprasto sveiko proto testo, kurio esmė užtikrinti, kad jis įrodo tik tuos dalykus, apie kuriuos žinome, kad jie teisingi. Jis neturėtų kartu įrodinėti dalykų, apie kuriuos žinome, kad jie neteisingi. Jei Vinay Deolalikaras negalės parodyti, kad jo įrodymas tenkina sveiko proto testą, tai tebus riebi antis.
P ir NP klasių tapatumas
Iš 7-ių Tūkstantmečio premijos problemų kol kas išspręsta tik Poincarė teorema. Dabar aprašysime dar vieną iš tų problemų.
P ir NP lygybės klausimas algoritmų teorijoje jau 30 m. yra viena pagrindinių neišspręstų problemų. Teigiamo atsakymo atveju tai reikštų, kad teoriškai įmanoma gerokai greičiau išspręsti daugelį sudėtingų uždavinių. Dabar sudėtingiausius NP uždavinius įmanoma išspręsti tik per eksponentinį laiką, kas nelabai priimtina. P ir NP klasių santykį nagrinėja skaičiavimo sudėtingumo teorija, kuri nagrinėja resursus, būtinus uždavinio sprendimui. Bendriausi resursai tai laikas (reikalingų atlikti veiksmų kiekis) bei atmintis.
Čia išsireiškimas trumpesnis laikas (greičiau) vartojamas tam, kad reikštų, jog sprendimą galima rasti per polinominį laiką,
t.y. P. Jei padidinsite uždavinio dydį, sprendimas užtruks ne daugiau kaip dydis, pakeltas kvadratu, kubu arba pakeltas tam tikru laipsniu.
Uždaviniai, kuriuos galima išspręsti per polinominį laiką, vadinami sudėtingumo klase P ir paprastai laikomi lengvais, tačiau atkreipkite dėmesį,
kad praktikoje jie vis tiek gali užtrukti ilgai, per ilgai. Uždaviniai, kurių sprendimas trunka ilgiau nei polinominis laikas (NP), yra tokie,
kad šiek tiek padidinus uždavinio dydį, gauname sprendimo laiką, palyginamą, tarkim, su Visatos gyvavimo trukme; t.y. NP uždaviniams sprendimo paieška
nepriskiriama P klasei, o korektiškumo patikra randasi toje klasėje.
NP paprastai suprantama kaip nedeterministinis polinomas, nes jei atspėjate teisingą sprendimą, jį galima patvirtinti per polinominį laiką.
Kitas būdas tai vertinti jei turite orakulą, kuris pateikia teisingą atsakymą, galite patikrinti, ar jis yra P. Taigi, susidaro tam tikras įspūdis,
kad NP uždaviniai yra beveik P, bet šis įspūdis išnyksta, kai pažvelgiate į tikrą NP uždavinį.
 Palyginkime n2 (polinominio, P) ir 2n (eksponentinio, NP)
sudėtingumo algoritmus. Padidinus duomenų kiekį dvigubai, P algoritmo trukmė padidėja 4 kartus. Tuo tarpu NP
algoritmo trukmė padidėja 4 kartus pridėjus tik 2 duomenų elementus.
Palyginkime n2 (polinominio, P) ir 2n (eksponentinio, NP)
sudėtingumo algoritmus. Padidinus duomenų kiekį dvigubai, P algoritmo trukmė padidėja 4 kartus. Tuo tarpu NP
algoritmo trukmė padidėja 4 kartus pridėjus tik 2 duomenų elementus.
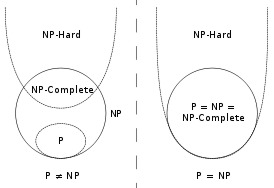
P Í NP, bet ar P=NP?
Kitaip tariant, jei per trumpą (polinominį) laiką galima patikrinti kokį nors konkretų atsakymą, tai ar reiškia, kad greitai (per polinominį laiką ir naudojant polinominę atmintį) galima rasti sprendimą?
Pavyzdžiui, ar tiesa, kad tarp skaičių {-2, -3, 15, 14, 7, -10,...} yra tokių, kurių suma lygi 0 (uždavinys apie poaibių sumas)? Atsakymas teigiamas, nes nesunku surasti, kad -2-3+15-10=0 (informacija, būtina teigiamo atsakymo patikrinimui, vadinama sertifikatu). Ar iš čia seka, kad taip pat lengvai bus parinkti šitie skaičiai? Ar patikrinti sertifikatą ir jį rasti yra tas pats sunkumas? Atrodytų, kad parinkti skaičius yra sunkiau.
P klasės pavyzdžiai:
- Ar žemėlapyje galima nuspalvinti šalis raudonai, žaliai ir mėlynai taip, kad jokios gretimos nebūtų tos pačios spalvos?
- Ar pateiktas dėžių kiekis tilps į sunkvežimį?
- Ar žinant atstumus tarp miestų, galima juos visus apvažiuoti apsilankant tik kartą, nuvažiuojant ne daugiau 5000 km?
Žinomiausias iš NP yra komivoježerio uždavinys: turime miestus ir atstumus tarp jų ir reikia rasti sprendinį,
susijusį su miestų aplankymu. Yra trys šio uždavinio variantai: 1) spendimo priėmimo (ar yra apkeliavimo atstumas,
mažesnis už D); 2) paieškos (trumpesnio už D maršruto radimas); 3) optimizavimo (rasti trumpiausią maršrutą).
Įdomu, kad kiekvienas šių variantų vadinamas komivoježerio uždaviniu mat jie susiję taip, kad 3) sprendimas duoda 2) sprendimą, o šio 1) sprendimą.
Sprendimo priėmimo uždavinys yra NP, nes jei reikia išsiaiškinti, ar yra turas, kurio atstumas yra mažesnis
už D, reikia patikrinti visus galimus turus pagal D, ir ši užduotis labai sparčiai auga didėjant miestų skaičiui
(jei yra n miestų, reikia patikrinti Tai galioja ir paieškos variantui, tačiau ne optimizacijai, kuriai reikia patikrinti visus maršrutus, todėl
jis yra NP. Tačiau jei atsiras liudininkas, sakantis, kad M yra trumpiausiasn maršrutas, galėsite pasakyti ar
tikrai, tik žinodami sprendinį (t.y. vis tek teks atlikti pilną paiešką). Kadangi optimizavimo uždavinio sprendimas
duoda sprendimą 1) ir 2), priklausantiems NP, jis vadinamas NP sunkiu.
Pirmąkart klausimą apie skaičiavimo sudėtingumą iškėlė K. Giodelis 1956 m. laiške Dž. fon Neimanui, kuriame klausė, ar gali uždavinys (kuris, kaip dabar žinoma, yra NP-pilnas) būti išspręstas per kvadratinį ar tiesinį laiką. Kartu Giodelis spėjo, kad jei sprendimas egzistuoja, tai leistų kompiuterio pagalba išspręsti nemažai matematinių problemų.
O klausimą apie P ir NP klasių lygybę pirmąkart iškėlė S. Kukas (1971) ir nepriklausomai nuo jo L. Levinas**) (1973).
Šiuo metu dauguma matematikų mano, kad tos klasės nėra lygios. Vinay Deolalikaras teigia tai įrodęs.
S. Aaronsonas, kartu su 2021 m. Abelio premijos laureatu Avi Wigdersonu,
2009-ais paskelbė straipsnį, kuriame nurodė naują kliūtį P klasė nėra ta pati kaip NP klasė (tai jau trečioji atrasta kliūtis).
Gerhard J. Woegingeris parengė 116 tariamų įrodymų per 1986-2016 m. laikotarpį sąrašą. Kai kurie tų tvirtinimų gavo medijų dėmesį V. Deolalikaro yra vienas tarp tų.
Kas jei NP = P? Tai gali reikšti tik tai, kad yra būdas rasti sprendimą, kuriam nereikia ieškoti visoje uždavinio erdvėje. Komivoježerio uždavinio atveju tai reiškia, kad galėtume pasakyti, ar yra turas, kurio ilgis mažesnis nei D, neieškodami visoje erdvėje. Kaip tai gali būti? Turėtų būti kažkokia lengvai apskaičiuojama savybė, leidžianti rasti sprendinį. Pvz., jei galėčiau įrodyti teoremą, kai duotas N miestų tinklas, kurio minimalus turas visada yra f(N) ilgio, kur f yra funkcija, kurią galime įvertinti per polinominį laiką, tai sužinojimui, ar yra turas trumpesnis nei D , tiesiog paskaičiuojama f(N) ir gauta reikšmė palyginama jį su D. Uždavinys išspręstas kaip P!
Bet žinoma, nėra tokios N funkcijos, kuri veiktų taip; jei tokia būtų, mes ją jau seniai būtume radę. Gal
net yra būtų įrodymas, kad tokia funkcija negali egzistuoti. Ir ji tikrai negali egzistuoti, jei P!=NP. Alternatyva
yra funkcija, leidžianti sumažinti paieškos dydį, t.y. nukreipiančioji funkcija. Tai panašu į euristikos idėją
t.y. taisyklę, leidžiančią pasirinkti variantus, kurie su didele tikimybe, bet negarantuotai duodančią gerą
sprendimą. Euristika galėtų būti kažkas panašaus į visada vykti trumpiausiu keliu į kitą miestą. Tokia euristika
praktikoje naudojama norint rasti protingus NP uždavinių sprendimus.
Euristika, kuri ne tik garantuoja, bet ir pateikia tikrąjį sprendimą, nėra euristika tai algoritmas, kuris
išsprendžia uždavinį. Jei algoritmas veikia P klasėje sprendžiant komivoježerio uždavinį, tada P = NP.
Problema atspindėta ir populiarioje kultūroje, pvz.:
Prieš 50 m. (1974 m.) E. Rubikas išrado savo kubą (ruošdamas aprašomosios geometrijos kursą ir galvodamas apie 5-is Platono kūnus).
Įdomu, kad jis turi Dievo skaičių, kuris yra 20 (bet ne 21, kuris yra akis :) ) - t.y. tiek ėjimų pakanka sudėlioti kubą iš bet kokios padėties (atseit, tik Dievas gali tai sugebėti!?)...
2017 m. įrodyta, kad uždavinys, kad per n ėjimų galima surinkti Rubiko kubą, yra NP išsprendžiamas.
P != PSPACE
Ne mažesnę svarbą už P!=NP teiginį turi ir P!=PSPACE. Šio klausimo svarba tame, kad jei P=PSPACE, tai ir P=NP.
Grubiai imant, PSPACE yra uždavinių klasė reikalaujančių vietos polinominiu masteliu čia vieta suprantama
atminties prasme, t.y. juostos ilgis, reikalingas Tiuringo mašinai.
Yra žinoma, kad laiką galima pakeisti atmintimi jei norite, kad programa veiktų greičiau, jai duokite daugiau atminties. Atrodom kad klasės P ir PSPACE yra kažkuo susijusios, tačiau ar jos yra lygios? T.y., jei uždavinį galima išspręsti per polinominį laiką, ar tai reiškia, kad jį galima išspręsti su polinomine atmintimi ir atvirkščiai.
P!=PSPACE įrodymui reikia surasti uždavinį, išsprendžiamą per O(n)SPACE, tačiau negali būti išsprendžiamas per O(nk) laiką visiems k > 1. Nesenas proveržis šio srityje yra tame, kad uždaviniai, kurie gali būti išsprendžiami su O(n)SPACE, reikalauja bent jau O(n2-e laiko. Ir nors tai neįrodo, kad P!=PSPACE, tačiau tai iliustracija, kad SPACE yra geresnis už laiką O(n), lyginant su blogiausiu atveju O(n2). Tai galima interpretuoti kaip atmintis vertingesnė už atmintį.
Skaičiavimų sudėtingumo teorijoje PSPACE uždavinių klasė apima sprendimų priėmimo uždavinius, kurie gali būti išsprendžiami Tiuringo mašinos pagalba su polinominiu atminties kiekiu (pradinių duomenų kiekio atžvilgiu).
Sprendimų priėmimo uždavinys yra laikomas PSPACE-pilnu, jei jis išsprendžiamas naudojant atminties kiekį,
polinominį pradinių duomenų kiekiui ir jei bet kuris uždavinys, išsprendžiamas polinominėje erdvėje, gali būti
transformuotas į uždavinį, išsprendžiama per polinominį laiką. Uždaviniai, kurie yra PSPACE-pilni, gali būti
laikomi sunkiausiais PSPACE klasės sprendimo priėmimo uždaviniais, nes bet kurio tokio uždavinio sprendimas
galėtų būti lengvai panaudotas bet kuriam kitam PSPACE uždaviniui spręsti.
Uždaviniai, žinomi kaip PSPACE-pilni, apima reguliariųjų išraiškų ir kontekstinių gramatikų savybių nustatymą, kiekybiškai įvertintų
Būlio formulių teisingumo nustatymą, laipsnišką kombinatorinio optimizavimo uždavinių sprendinių keitimą ir daugybę galvosūkių bei žaidimų.
*) Stivenas Kukas (Stephen Arthur Cook, g. 1939 m.) - amerikiečių kompiuterių mokslo atstovas, Toronto un-to (Kanadoje) profesorius (nuo 1970 m.). Laikomas vienu skaičiavimų sudėtingumo teoorijos pradininkų. 1982 m. gavo Tiuringo premiją už indėlį į šią sritį. 1971 m. straipsnyje formalizavo polinominio laiko redukciją (vadinamą jo vardu) ir įrodė, kad Bulio funkcijų įvykdomumo uždavimys yra NP-pilnu.
**) Leonidas Levinas (g. 1948 m.) - ukrainiečių kilmės amerikiečių matematikas, besispecializuojantis skaičiavimų sudėtingumo srityje. Į JAV emigravo 1978 m., yra Bostono un-to profesorius. Kandidato 5 daktarus laipsnio 1971 m. ginant disertaciją vadovaujant A. Kolmogorovui, negavo dėl neapibrėžtų politinių pažiūrų, Žinomas darbais apie skaičiavimų atsitiktinumą, algoritminį sudėtingumą ir neišsprendžiamumą, matematikos pagrindus ir kt. Nepriklausomai nuo S. Kuko 1971 m. įrodė Kuko-Levino teoremą, kurios dėka suformuluota P ir NP klasių lygybės problema. Už tai 2012 m. jam skirta Knuto premija.
Algoritmų sudėtingumas
Polinominio sudėtingumo uždaviniai
Paimkime dviejų matricų sandaugą C=AB
kuri skaičiuojama taip: cij = SUM(aik bkj), k kintant nuo
1 iki n, kiekvienam i ir j tarp 1 ir n.
Taip viso atliekama n3 daugybos ir n2(n-1) sudėties operacijų, o bendrai - 2 n3-n2 aritmetinių veiksmų.
O ar galima dvi matricas sudauginti greičiau? O taip! Panaudojus Štraseno algoritmą, atliekama O(nlog 7) veiksmų.
Uždaviniai, kurių sprendimui žinome polinominio sudėtingumo [ O(np ] algoritmus, yra išsprendžiami net tada, kai n >> 1 (aišku, kai p nėra labai didelis skaičius):
- tiesinės algebros uždaviniai;
- tikrinių reikšmių paieška;
- matematinės fizikos užduotys;
- kiti...
Nepolinominio sudėtingumo uždaviniai
Imkim n skirtingų objektų (a1, a2, ... an).
Reikia sugeneruoti visus skirtingus jų dėstinius (kėlinius):
Pn = {( a1, a2, ... an)}
Skirtingų kėlinių yra n!, todėl net efektyviausių algoritmų sudėtingumas O(n!).
Pagal Stirlingo formulę įvertiname:
n! = sqrt(2 pi n) (n/e)n
Tada kėlinių Pn generavimo laikai (apytiksliai):
T(11) = 0.28 (s); T(12) = 3.4 (s); ...
T(17) = 29.5 (d); T(18) = 532 (d); ...
O T(20) jau 553 metai (!)
O jei panaudosime lygiagrečiuosius algoritmus? Su 2056 procesoriais T(20) būtų apie 3 mėn., tačiau P21 sugaištume ilgiau nei 5 m.
NP sudėtingumo uždaviniai
Palyginkime n2 ir 2n sudėtingumo algoritmus.
Padidinus duomenų skaičių dvigubai, polinominio sudėtingumo algoritmų veikimo trukmė padidėja
keturgubai.
Eksponentinio sudėtingumo algoritmų veikimo trukmė padidėja du kartus pridėjus vos vieną vienintelį duomenį.
NP (angl. nondeterministic polynomial time) uždavinių klasė tokia, kuriai nežinome polinominio sudėtingumo sprendimo algoritmų, tačiau atlikę O(nk) veiksmų, galime patikrinti, ar duotasis objektas yra uždavinio sprendinys.
Aišku, kad P < NP, tačiau ar P <> NP?
Ši problema yra ir tūkstantmečio problemų sąraše (iš kurio teįrodytas tik Puankarė teiginys); apie ją daugiau žr. >>>>
Papildomai skaitykite:
Jų begalinė išmintis
Tūkstantmečio problemos
Žmonės prieš kompiuterius
Žaidimų teorijos panaudojimas
Iniciatyva: Matematikos keliu
Amerikai matematika nereikalinga!
Šriodingerio katinų dresiravimas: kvantiniai kompiuteriai
Netiesinis mąstymas: išspręsti neišsprendžiamą
Simpsonų trauka ir žaidimas skaičiais
Intuityvus Hafmano kodo paaiškinimas
Matematikos ir fizikos šmaikštumai
A. Puankarė. Mokslas ir hipotezė
P. Fejerabendas prieš mokslą
Kur viešpatauja chaosas?
Meilės sinusoidė
Matroidai
Lankytojų komentarai / pastabos
Mums pastabas, kurias pateikiame žemiau, 2012 m. gegužės 1 d. atsiuntė Žilvinas. Tai mus paskatino įvesti šiame straipsnelyje atsiliepimų skyrelį, kuriame jūs galite diskutuoti, pateikti savo pastabas, papildyti šią temą...
Žilvino žinutė:
Skyrelyje: P ir NP klasių tapatumas
Klaida fragmente:
Palyginkime n^2 (polinominio, P) ir 2^n (eksponentinio, NP) sudėtingumo algoritmus.
Padidinus duomenų kiekį dvigubai, P algoritmo trukmė padidėja 4 k.
Tuo tarpu NP algoritmo trukmė padidėja 4 k. pridėjus tik 2 duomenų elementus.
Taisymas:
Pirmiausia iš pradžių kalbama apie dvigubą pradinių duomenų padidinimą (2*n), vėliau apie
padidinimą dviem elementais (n+2),
jeigu pradiniai duomenys yra didinami dvigubai, tai P algoritmo trukmė padidėja 4 kartus,
o NP algoritmo 2^n kartų (ne 4 k). Jeigu kalbama apie pradinių duomenų padidinimą dviem elementais,
tai P algoritmo veikimo laikas padidėja (n^2 + 4*n + 4)/(n^2) k (kuo didesnis n tuo algoritmo veikimo laikas
labiau priklauso nuo
n^2 atliekų operacijų, kas sąlyginai yra nedaug). Tuo tarpu NP (2^n) padidinus dviem elementais laikas
padidėja (2^(n + 2))/(2^n) k => 4 k
(kas reiškia, kad su kiekvienu n padidėjimu laikas padidėja dvigubai). Kaip pavyzdį galima pasirinkti konkrečią situaciją:
tarkime turite NP algoritmą, kuris su n = 1 darbą atlieka per 2s, tačiau jeigu n pasirinksite 1000,
algoritmo veikimo laikas padidės 2s*2^1000 >= 10^300 s kas yra apytiksliai 10^292 metų.
Jeigu būtų įrodyta, kad P = NP tai reikštų, kad galima nulaužti visas dabartines bankų saugumo sistemas,
nes jos remiasi tuo, kad žinant savo slaptažodį ir login patikrinti ar jis teisingas užtrunka tiek
kiek trunka įvykdyti P klasės algoritmą (sąlyginai trumpai), tačiau nori atspėti
slaptažodį reikia vykdyti NP kalsės algoritmą ir išmėginti visus įmanomus variantus,
kas iš pavyzdžio tampa aišku, kad užimtų didžiulius kiekius laiko.
Tikiuosi pavyzdys padėjo suprast P ir NP tapatumo problemą. :)
Papildomai skaitykite:
Tiuringas liūdno likimo genijus
Ar jau rūksta dūmai? Navier Stokes lygtys
Paradoksai sulig dirbtiniu intelektu
Kviečiame bendrauti!
Lankytojų žinutės
Doctor Haris Lacan 2020 m. kovo 10 d., antradienis, 14:26:10
Jeigu ant sveiko proto ribu ;))
tai materija=25 25= mintis ;))o mintis, ir samone...
=projekcija? tai nesakiau, jog uz isivaizdavimo ribu...
irgi nieko nera?. yra samone, kuria suprojektavo...
Samones__filosofija!!!!!!!!!!.
DrHarisLacan 2018 m. rugsėjo 7 d., penktadienis, 21:41:10
Isivaizdavimas priklauso, tik nuo manes.
;]]]]]]].
DrHarisLacan 2018 m. rugpjūčio 17 d., penktadienis, 18:51:28
Dar yra isivaizdavimas, ir realybe, kurie yra simuliuojamos realybes santykyje..........., Jeigu isnyktu ribos]. to nera. to neisivaizduojame, ir to nematome;) tada x-5+12r= ? spindulys nusitestu, iki naujos matricos!.
sisteminamas, ir determinuojamas matematines, ir simbolines kalbos analogiskumas, ir materialistiniaj sinusaj., dar.. tekme pasiskyrsto abstrakcioje terpej[..........., jeigu nebutu kazko'''''''''''? ar neisnyktu ensteino realybe?.
DrHarisLacan 2018 m. rugpjūčio 3 d., penktadienis, 22:58:39
Jeigu nezinote, ar nemastote, ar tiesiog negalite isivaizduoti.........., visa santyki peremu materialiaj, ir determinuoju..........,
Dr Haris Lacan 2018 m. liepos 15 d., sekmadienis, 08:22:06
Gatvėmis vaikšto ateities vaikai jie skaito mano mintis.
Aš nemoku gražiai kalbėti, jų akys viską tau pasakys.
Juk mano žodžiai lyg peiliai į širdį, o meilė saldi kaip mirtis.
Jei tu netiki, pažvelk, pažvelk į jų akis.
HarisLacan 2017 m. gruodžio 18 d., pirmadienis, 13:12:41
tai surrealizmas irgi iveina, i fraktalo ir fibonacci skaiciu sekos grafikus, ar ne?:).