Laimėti pralaimint: sprendžiamas „dviejų vokų“ paradoksas. Vartiklis

Vieno voko turinio sužinojimas gali pasakyti daugiau nei galima pagalvoti. Atsitiktinis pasirinkimas, priklausomai nuo jame esančios sumos, gali žaidėjui padėti laimėti daugiau. M. McDonnel'is ir D. Abbott'as iš Australijos sukūrė naują strategiją, kuri yra naujas žingsnis sprendžiant, atrodytų, paprastą, tačiau dar neišspręstą vadinamąjį „dviejų vokų“ paradoksą.

D. Abbott

M. McDonnel

Nors žaidėjas, atsitiktinai keičiantis strategiją, gali žinoti ankstesnių žaidimų statistiką apie sumas vokuose, ši informacija nėra būtina. Analizė rodo, kad visada galima padidinti laimėjimą panaudojant Cover‘io metodą, nežinant „namų ribos“ (didžiausios laimėjimo sumos) ir statistinio skaičių pasiskirstymo. Tai panašu į tai, ką inžinieriai vadina „aklu optimizavimu“.

„Dviejų vokų“ paradokse žaidėjas turi rinktis tarp dviejų vokų, kurių viename yra dvigubai didesnė suma nei kitame. Žaidėjas, pasižiūrėjęs vieno voko turinį, gali nuspręsti imti kitą. Kaip elgtis? Atrodytų, kad tikimybė yra vienoda: 1/2. Tačiau kažkodėl tikimybių teorija tikina, kad visada verta pakeisti voką.

Tarkim, pirmame voke yra 10 lt. Tada antrame gali būti 20 arba 5. Laikydami tikimybę vienoda (1/2), galima paskaičiuoti laukiamą sumą: 0,5 * 5 + 0,5 * 20 = 12.5. Kadangi 12,5 daugiau nei 10, labiau apsimoka rinktis antrą voką – ir tada, atseit, ilgai žaidžiant bendras laimėjimas būtų 12,5 Lt. Ir tai visiškai nepriklauso nuo pradinės sumos – imant antrą voką visada laimima 5/4 daugiau nei yra pirmajame voke.

Tačiau intuicija sako ką kitą – apie principinę lygybę abiejų vokų atžvilgiu; juk sukeitus voką samprotauti galima lygiai taip pat. Tame ir glūdi paradokso esmė. Šį paradoksą išspręsti matematikai bando nuo pat 20 a. 4-o dešimtm., nors „dviejų vokų“ formuluotę tik 1988 m. jam suteikė Harvardo prof. Sandy Zabell'is¹⁾. Nors keletas mokslininkų paskelbė radę sprendimą, konsensusas nėra priimtas ir problema tebelaikoma neišspręsta.

Matyt „dviejų vokų“ paradokso esmė tame, kad, kai žaidėjas pažiūri į pirmą voką, simetrija pažeidžiama, nes vokai tampa nelygiaverčiais. Australų mokslininkai savo metodą pavadino Cover‘io strategija, nes jį 2003 m. pietų metu pasiūlė Stanfordo prof. Tom Cover‘is. Žaidėjas atsitiktinai keičia voko pasirinkimo strategiją priklausomai nuo pirmame voke esančios sumos. Kuo didesnė suma, tuo su mažesne tikimybe jis ima kitą voką (net nežinodamas, kokios yra sumų ribos). Simuliacija rodo tokios strategijos efektyvumą. Įdomiausia, kad toji strategija veikia ir tada, kai žaidėjas nusprendžia nekeisti vokų, kai pirmo voko sumą didesnė už kažkokią paties žaidėjo nusistatytą sumą (o šios, savaime aišku, žaidimo organizatoriai nežino).

D. Abbott'as aiškina, kad jam padėjo patirti dirbant su Brauno reketu (sumąstytu R. Feinmano ir esantis atskiru „Maksvelo demono“ atveju – juos siekiama paneigti antrąjį termodinamikos dėsnį, t.y., atlikti naudingą darbą nesant temperatūrų skirtumo ir tik vidinės energijos pagalba). Reketas veikia taip: yra dvi kameros su dujomis, kurias jungia miniatiūrinis velenas (dirbantis be trinties, kurio viename gale yra ratas su mentėmis (dešinėje), o kitame dantratis su stabdžiu. Tarp kamerų ant veleno pakabintas svoris. Stabdis leidžia velenui suktis tik viena kryptimi – tai ir yra simetrijos pažeidimas. Kairės kameros dujos chaotiškai atsitrenkia į mentes, tačiau pasukti veleną gali tik viena kryptimi – ir jis ima lėtai kelti svorį vien tik pirmos kameros molekulių šiluminės energijos dėka. Brownian ratchet

Tiesa, fiziškai tokio reketo sukurti neįmanoma, - ir tai paaiškino pats R. Feinmanas. Mat stabdis turi būti pakankamai mažas, kad sureaguotų į atskirų molekulių smūgius į mentes. Todėl jis sėkmingai svyruos ir nuo „savojo“ Brauno judesio, laikas nuo laiko atsidarydamas ir leisdamas pasisukti velenui atgal. Feinmanas paskaičiavo, kad kamerose esant vienodoms temperatūroms, judesiai pirmyn ir atgal vieni kitus anuliuos, t.y. velenas nesisuks.

Įdomus „dviejų vokų“ paradokso palyginimas su Parondo paradoksu: paėmus du atsitiktinius žaidimus, kurių kiekvieną atskirai galima lengviau pralaimėti, nei laimėti, galima sukurti laiminčiąją strategiją, kai žaidimai žaidžiami pakaitomis.

Tarkim, turime pradinį kapitalą. Tada kaskart jį papildome arba sumažiname 1 Lt, priklausomai nuo monetos mėtymo. Tik visa gudrybė tame, kad moneta nėra simetrinė (t.y., jos vienos pusės atsivertimo tikimybė nėra 1/2). Iš tikrųjų žaidžiami du žaidimai. Žaidime B turime dvi monetas (M1 ir M2), kurios skiriasi tik pusių atsivertimo tikimybėmis. Ir pasirenkamas kažkoks skaičius K bei įvedama taisyklė: jei kapitalas yra kartotinis K, tai metam monetą M1, o jei nekartotinis – M2.

Pasirenkame tokias tikimybes, kad abu žaidimai mums būtų pralošiami. Abotas parodė, kad taip yra, pvz., kai žaidime A mums palankios pusės tikimybė 0,5-E (kai E=0,005), o M1 ir M2 mums palankios tikimybės yra 1/10-E ir ¾-E (ir K = 3). Tačiau žaidimų kaitaliojimas leidžia laimėti – tiesa, ne bet kokie kaitaliojimai, o tik tam tikri, pvz., ABBABB...

T. Cover

Šis paradoksas paneigiamas tuo, kad abu žaidimai tarpusavyje susiję – ir būtent per vos ne mistinį skaičių K. Juk jį įvedus B žaidimas tampa priklausomas nuo žaidimo A. O toliau viskas griežtai pagal tikimybių teorijos dėsningumus.

Panašus optimizavimo metodas sutinkamas investavime į akcijų rinką. Pvz., „lakių skysčių pumpavimas“. Jei turima kokia nors informacija apie rinkas (kompanijų finansinė būklė, teismai, apelsinų derlius, naftos telkinio atradimas). O jei nežinoma niekas?
Tada geriausia prekiauti akcijomis chaotiškai siekiant nedidelio prieaugio (pirkau pigiau-pardaviau brangiau) – visiškai nesirūpinant, ar tuo momentu gavote didžiausią pelną ar praleidote šansą dar labiau praturtėti.

Šios naujos įžvalgos gali paveikti daugelį teorinių ir praktinių sričių: termodinamikos, technologinių sistemų optimizavimo, elektroninių schemų tobulinimo, finansų ir kt. Nenuostabu, kad Abotas žinomas ir kaip stochastinio rezonanso (naudingo periodinio signalo sustiprinimas netiesinėse sistemose papildžius signalą „baltuoju“ triukšmu) tyrinėtojas.

Kartu šio paradokso nagrinėjimo įžvalgos iškėlė ir naujų klausimų: pvz., žaisdamas keletą žaidimų iš eilės, žaidėjas turėtų nuolat tikslinti strategiją atnaujindamas tikėtiną sumų pasiskirstymą vokuose. Ir kažkuo visai tai ima priminti „Šrėdingerio katino“ situaciją (žr. >>>> ), - ar tik neprisikasame prie gamtos dėsnių pagrindų?!

Žr. M.D. McDonnell, D. Abbott. Randomized switching in the two-envelope problem// Proceedings of the Royal Society Australia

Tai vienas iš paradoksų (tiksliau, loginių uždavinių) tikimybių teorijos srityje, parodantis, kad intuityvus („sveiko proto“) svarstymas gali būti klaidingas. Iš tikro, jis nėra paradoksu, nes savyje neturi vidinių prieštaravimų. Jis pavadintas „Sudarom sandorį“ žaidimų šou vedėjo Monty Hall’o³⁾ vardu, tačiau pateiktas (ir išspręstas!) Berklio Kalifornijos un-to biostatistikos prof. Steve Selvin‘o (g. 1941 m.) 1975 m. laiške „The American Statistician“ žurnalui. Uždavinys ypač išpopuliarėjo po pasirodymo 1990 m. „Parade“ žurnalo Marilyn vos Savant⁴⁾ rubrikoje „Paklausk Merilinos“.

„Tarkim, vedėjas tau pasiūlo žaidimą. Prieš tave trys durys, kurių vienas reikia pasirinkti. Už vienų durų automobilis (tarkim „Lamborghini“, kurį gausi, jei atspėsi), už kitų dviejų ožys (arba juokdarys, rodantis tau špygą, - kurią gauni, jei tas duris pasirinkai). Vedėjas žino, už kurių durų kas yra. Tau pasirinkus kažkurias duris, vedėjas (nepriklausomai nuo tavo pasirinkimo) atidaro kažkurias kitas duris, už kurių visada randasi ožys. Tada jis klausia, ar nori pasilikti savo ankstesnį spėjimą, ar jį pakeisti. Kaip elgtis – likti prie savo pasirinkimo ar jį keisti?

Iš pirmo žvilgsnio, t.y. intuityviai, atrodytų, kad šansai, kurias duris po pasiūlymo rinksiesi, yra absoliučiai vienodi (t. y. abiem atvejais tikimybė 1/2). Taip ir būtų, jei ateitų visiškai pašalinis žaidėjas, visiškai nežinantis apie ankstesnius veiksmus, ir jam pasiūlytų tiesiog rinktis iš dviejų durų. Tačiau mūsų žaidėjas turi papildomą informaciją – tad ar gali ši jam padėti padidinti šansus?!

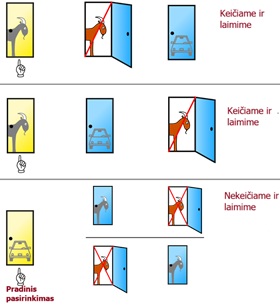
Pasirodo, kad taip! Detali analizė rodo, kad žaidėjas padvigubina šansus keisdamas ankstesnį pasirinkimą (t.y., tokiu atveju jis įgyja 2/3 tikimybę). Trijų durų paradoksas

Tarkim kad renkamasi pirmos durys. Tada galimos tokios kombinacijos:

Už pirmų durų	Už antrų durų	Už trečių durų	Jei pasiliekame pirmas duris	Jei pradinis pasirinkimas keičiamas
Ožys	Ožys	Automobilis	Gauname ožį	Laimime automobilį
Ožys	Automobilis	Ožys	Gauname ožį	Laimime automobilį
Automobilis	Ožys	Ožys	Laimime automobilį	Gauname ožį

Taigi, likus prie ankstesnio pasirinkimo, laimime tik kartą iš trijų variantų, o pakeitus pasirinkimą – dukart. Kitas būdas uždavinio sprendimo supratimui – abi pirmą kartą nepasirinktas duris laikyti kaip vieną esybę.

Bet iš kur žaidėjas gauna papildomos informacijos lyginant su pradine situacija? Juk jos nesuteikia vedėjas. Iš tikro, durų pasirinkimo pakeitimas skiriasi nuo atsitiktinio pasirinkimo tuo, kad jis naudojasi ankstesne informacija. Vis tik didesnė dalis „Parade“ skaitytojų atsisakė patikėti sprendimu – apie 10 tūkst. skaitytojų parašė žurnalui, kad M. vos Savant klysta. Net labai iškilus matematikas Paul Erdos’as tol netikėjo, kol jam nebuvo parodyta kompiuterinė sprendimo simuliacija.

Trijų durų uždavinys artimai susijęs ne tik ir su ankstyvu Bertrano trijų dėžių su monetomis uždaviniu (Joseph Bertrand’o⁵⁾ pateiktu 1889-ais), bet ir trijų kalinių uždaviniu, M. Gardnerio pasiūlytu 1959-ais:

Trys kaliniai (pažymėkime juos K₁, K₂ ir K₃), nuteisti mirties bausme, kali vienutėse. Prezidentas atsitiktinai vienam skiria malonę. Prižiūrėtojas žino, ką pasirinko prezidentas, tačiau neturi teisės tai pasakyti. Tačiau K₁ prašo jo pasakyti, kuriam iš kitų dviejų bus tikrai įvykdyta mirties bausmė: „Jei malonė suteikta K₂, pasakyk man, kad K₃, jei pasigailėta K₃, pasakyk K₂. Jei pasigailėta manęs, mesk monetą ir pasakyk bet kurį“.
Prižiūrėtojas pasako, kad nubaustas bus K₂. K₁ apsidžiaugia, nes dabar jo šansai išgyventi padidėja nuo 1/3 iki 1/2. Jis slapta tai pasako K₃, kuris taip pat apsidžiaugia, nes vis dar laiko, kad K₁ išgyvenimo tikimybė 1/3, o jo – išaugo iki 2/3. Kaip tai nutiko?!

¹⁾ Sandy L. Zabell'is - matematikos profesorius Harvardo universitete. Daktarinę disertaciją apsigynė 1974 m. Pagrindinė tyrimų sritis - tikimybių teorija (atskiru atvedu, didelių nuokrypių teorija) ir Bajeso statistika (atskiru atveju, sukeičiamumo (exchangeability) tyrinėjimai). Domisi istorija, matematine logika, DNR identifikavimu, filosofiniu pagrindimu, komunikacijų saugumu ir tikimybių bei statistinių metodų taikymu teisėje.

²⁾ Morisas Kraičikas (Maurice Kraitchik, 1882-1957) – žydų iš Minsko kilmės belgų matematikas ir matematikos populiarintojas. Jo pagrindinės domėjimosi sritys buvo skaičių teorija ir laisvalaikio matematika. 1931-39 m. redagavo laisvalaikio matematikai skirtą žurnalą „Sfinksas“. Antrojo pasaulinio karo metais emigravo į JAV. Jis išgarsėjo 1953 m. pasiūlęs „dviejų vokų“ paradoksą:

Du vienodai turtingi žmonės susitinka, kad palygintų savo piniginių turinį. Kiekvienas jų nežino kiek yra pinigų kiekvienoje piniginėje. Žaidimas vyksta taip: kurio piniginėje mažiau pinigų, gauna kito piniginę (jei lygu, nieko neįvyksta). Kiekvienas jų gali mąstyti taip: „Tarkim, aš turiu A savo piniginėje, tad daugiausiai aš galiu prarasti A. Jei laimėsiu, ko tikimybė yra 0,5, tai turėsiu daugiau nei 2A. Tad žaidimas yra man naudingas“. Kitas mąsto lygiai taip pat. Tai kur klaida jų samprotavimuose?

³⁾ Montis Holas (Monty Hall, pilna pavardė Halparin , 1921-2017) – žydų kilmės kanadiečių TV ir radijo laidų vedėjas, 1955 m. persikėlęs į JAV, kur dėmesį sutelkė žaidimų šou. Nuo 1963 m. geriausiai žinomas kaip „Sudarom sandorį“ šou vedėjas, su kuriuo vienaip ar kitaip buvo susijęs iki gyvenimo pabaigos. Jo vardas suteiktas galvosūkiui apie tris duris. Aktyviai užsiėmė ir filantropija.

⁴⁾ Merilina vos Savant (Marilyn vos Savant, g. 1946 m.) - amerikiečių žurnalis, rašytoja, dramaturgė, į Gineso rekordų knygą įtraukta kaip turėjusi aukščiausią IQ. Nuo 1986 m. „Parade“ žurnale vedė „Paklausk Merilinos“ skiltį, kur sprendė galvosūkius ir atsakinėjo į klausimus. Joje 1990-ais buvo išpopuliarintas ir Mončio Holo uždavinys. Kai Andrew Wiles paskelbė, kad įrodė Didžiąją Ferma teoremą, ji išleido knygą „Garsiausios matematikos problemos“ (1993), kurioje apžvelgė jų istoriją; pratarmę jai parašė M. Gardneris.

⁵⁾ Žozefas Bertranas (Joseph Louis Francois Bertrand, 1822-1900) - prancūzų matematikas ir mokslo istorikas, darbavęsis skaičių teorijos, diferencialinės geometrijos, tikimybių teorijos, ekonomikos ir termodinamikos srityse. 1845 m. iškėlė hipotezę apie bent vieno pirminio skaičiaus egzistavimą intervale tarp n ir 2n-2, kai n > 2 (žr. Bertrano postulatas), kurią 1850 m. įrodė P. Čebyševas. 1849 m. pirmasis apibrėžė realius skaičius naudodamas Dedekindo pjūvį. Garsėjo ir tikimybinių ir ekonominių paradoksų formulavimu. Ekonomikoje peržiūrėjo oligopolijos teoriją; jo sukurtas konkurencijos modelis rodo, kad kainų konkurencijos sąlygomis Kurno išvados neveikia.