Eudoksas iš Knido

Eudoksas iš Knido (Eudoxos ho Knidios, 410/408 – 355/347 m.pr.m.e.) – graikų astronomas, matematikas, gydytojas, Platono mokinys. Išvystė proporcijų teoriją, ypač sąryšyje su iracionaliųjų skaičių nagrinėjimu, įvedė dydžio sąvoką ir pateikė pirmą rimtą įrodymą susijusį apskritimo kvadratūra. Jis nustatė, kad piramidės ar kūgio tūris yra trečdalis jų ploto padauginto iš aukščio.
Apie Eudoksą taip pat skaitykite >>>>>

Jo vardu pavadinta kreivė (Eudokso kampylė):
a²x⁴ = b⁴ (x² +y²)

Žinios apie jį pasiekė iš antrinių šaltinių, pvz., Arato poemos apie astronomiją. Teodosijaus iš Bitinijos „Sferiniai kūnai" galėjo remtis Eudokso veikalu. Jo vardu pavadinti krateriai Mėnulyje ir Marse.

Eudoksas gimė Knide, esančiame Mažojoje Azijoje. Pradžioje jis keliavo į Tarentą, kad mokytųsi matematikos pas Archytą. Būdamas Italijoje, jis apsilankė Sicilijoje, kur pas Filistoną mokėsi medicinos. Apie 387 m. pr.m.e., būdamas 23 m. amžiaus, jis su gydytoju Theomedonu nuvyko į Atėnus, kad mokytųsi su Sokrato pasekėjais. Pasėkoje jis tapo Platono mokiniu, pas kurį mokėsi kelis mėnesius, bet dėl nesutarimų išsiskyrė. Eudoksas buvo visiškai vargšas ir įstengė samdyti būstą tik Pirėjuje. Į Platono užsiėmimus jis kasdien eidavo 7 mylias. Jo draugai surinko pinigų, kad jis galėtų vykti į Heliopolį, esantį Egipte, kad galėtų tęsti astronomijos ir matematikos studijas. Ten jis gyveno 16 mėn. iš ten jis nuvyko į prie Marmuro jūros esantį Kiziką ir po to į Propontį. Tada keliavo į pietus į Moussolus rūmus. Pakeliui jis susirinko nemažai mokinių.

Apie 368 m. su mokiniais atvyko į Atėnus. Tada grįžo į gimtąjį Knidą, kur dirbo miesto taryboje. Čia pastatė observatoriją, rašė ir skaitė paskaitas teologijos, astronomijos ir meteorologijos temomis. Jis turėjo sūnų Aristagorą ir tris dukteris.

Astronomijoje jo indėlis yra astronominio gaublio įvedimas bei planetų judėjimo samprata. Jo veikalas apie proporcijas (ypač sąryšyje su iracionaliųjų skaičių nagrinėjimu) rodo gilią įžvalgą matematikoje. Taip pat Eudoksas išvystė Antifono priartėjimo metodą, meistriškai naudotą (Archimedo.

Senovės Graikijos matematikai skaičiavo kitaip nei mes. Jie nenaudojo dydžių ir lygčių, o naudojo proporcijas tarp dydžių. Tad jiems dviejų dydžių santykis buvo ne tiesiog skaičius, kaip mums, o santykinis ryšis tarp jų. Eudoksas suformulavo dviejų proporcijų lygybės apibrėžimą, kurį, trumpai išsireiškus šiuolaikine kalba, galima apibrėžti taip: a/b = c/d, jei bet kuriems sveikiems m ir n, ma ir nb santykis (daugiau lygu ar mažiau) yra toks pat kaip mc ir nd (jei ma > nb, tai ir mc > nd ir t.t.).

Taipogi, astronomija buvo laikoma matematikos šaka – astronomai kurdavo geometrinius modelius, kurie turėjo atkurti regimus dangaus kūnų judėjimus. Išliko kai kurie Eudokso veikalų pavadinimai: „Saulės pradingimas", „Oktaeteris" (apie Saulės-Mėnulio 8 m. kalendoriaus ciklą), „Phaenomena" bei „Entropon" (apie sferinę astronomiją), „Apie greičius" (apie planetų judėjimus).

Eudoksas kiekvienai planetai priskyrė vieną į kitų įdėtų sferų rinkinį. Prsikiriant sferų ašių pakrypimus ir skirtingus sukimosi periodus, jis galėjo aproksimuoti regimas planetų judėjimo ypatybes. Pvz., Mėnulis turėjo tris sferas: a) išorinė sukosi į vakarus 24 val. periodu (leido paaiškinti patekėjimą ir nusileidimą); b) vidurinė į rytus apsisuka kartą per mėnesį (paaiškina Mėnulio kelionę per Zodiaką); c) trečioji irgi apsisuka kartą per mėnesį, tačiau jos ašis nežymiai pakrypusi (tai paaiškina nukrypimus nuo ekliptikos ir mėnulio mazgų judėjimus).

Saulė irgi turėjo tris sferas, o 5-ios regimos planetos – po keturias. Vėliau Kalipas (4 a.) 27-ias Eudokso sferas papildė dar septyniomis, Aristotelis tarp judančių sferų įtraukė „nejudančias" sferas, kad vienų sferų judėjimas nepersiduotų kitoms.

Eudokso sistemos trūkumas buvo tame, kad ji negalėjo paaiškinti planetų ryškumo kitimų (nes sferos yra kocentrinės, todėl planetos visada yra vienodu atstumu nuo Žemės). Tai Antikos laikais nurodė Autolikas iš Pitanės. Astronomai atsakė įtraukdami deferentą ir epicikliką, kurie leido keistis planetų atstumui nuo Žemės.

---

Priedai: kreivės

Eudokso kampylė

Eudokso kampylė (graikiškai reiškia tiesiog „kreivė", „lenkta linija") – kreivė, kurią tyrinėjo Eudoksas iš Knido (apie 408-347 m. pr.m.e.), spręsdamas kubo padvigubinimo uždavinį. Jos lygtis Dekarto koordinatėse:
x⁴ = x² + y²
arba poliarinėse koordinatėse

Hipopedė

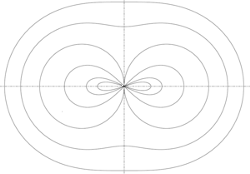
Hipopedė (graikiškai reiškia „arklio kanopa") – kreivė, kurią tyrinėjo Proklas, Eudoksas, o neseniai ir J. Booth (1810-1878). Jos lygtis Dekarto koordinatėse:
(x² + y²)² + 4b(b-a) (x² + y²) = 4b²x²
arba poliarinėse koordinatėse

Kai b = 2a, hipopedė atitinka Bernulio lemniskatę.

Kvadratriksė

Kvadratrisė (nuo lot. quadrator - kvadratintojas) – kreivė, panaudojama kitos kreivės ribojamo ploto (arba kvadratūros) nustatymui. Žinomiausios šios klasės kreivės yra Dinostrato ir E. W. Tschirnhausen'o, ir abi jos susijusios su apskritimu.

Dinostrato kvadratrisę (taipogi vadinama Hipijo kvadratrise) neblogai žinojo senovės graikai, ją minėjo Proklas, priskyręs kreivę Sokrato amžininkui, matyt, Hipijas iš Elėjos. Dinostratas, geometras ir Platono mokinys, nagrinėjo ją ir parodė, kaip ji panaudojama skritulio kvadratinimui. Papusas savo „Rinkiniuose" pristatė jos istoriją ir pateikia du būdus, kaip ji gali būti nubrėžta:

1) Ant apskrito cilindro nubrėžiama spiralė, tada gaunamas paviršius brėžiant linijas iš kiekvieno spiralės taško statmenai jos ašiai. Ortogonali šio paviršiaus dalies projekcija plokštuma, kurioje yra vienas statmenų ir pakrypusi į ašį ir yra kvadratriksė.

2) Ant cilindro, kurio pagrindas yra Archimedo spiralė kertamas apskrito kūgio. Nuo kiekvieno susikirtimo kreivės taško brėžiamos statmenos linijos brėžiamos į ašį. Bet koks plokštumos pjūvis duoda kvadratrisę.

Dar vienas nupiešimas yra toks. ABC yra skritulio kvadrantas. Lankas AC ir atkarpa AB padalija į vienodą lygių dalių kiekį. Iš centro brėžiami spinduliai iki lanko padalijimo taškų ir juos kerta linijos, lygiagrečios BC ir einančios per atitinkamus AB padalijimo taškus. Jų susikirtimo kreivė yra kvadratrisė.

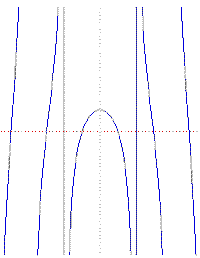
Dinostrato kvadratrisės lygtis Dekarto koordinatėse yra y = x cot 2a'
Iš čia matosi, kad kreivė yra simetrinė y ašies atžvilgiu ir sudaryta iš centrinės dalies, nuo kurios atsišakoja begalinis šakų skaičius. Asimptotės yra x = 2na, kur n - sveikas skaičius. Ašis y kertama 2a / 7r, tad, teisingai nubrėžta kreivė gali būti panaudota skritulio kvadratinimui. Ją taip pat galima panaudoti ir kubo padvigubinimo bei kampo dalijimo į tris dalis uždaviniams spręsti.

Tschirnhausen'o kvadratrisė irgi pradedama piešti kvadranto lanką ir spindulį padalinant į vienodą lygių dalių skaičių. Linijų, nubrėžtų iš lanko padalijimų bei lygiagrečių AB, bei linijų, lygiagrečių BC per AB padalijimų taškus, susikirtimas yra kvadratrisė.
Lygtis Dekarto koordinatėse yra y = cos 2a.
Kreivė periodinė ir x ašį kerta taškuose x = (2n-1)a, kur n yra sveikas skaičius. Jos savybės panašios į Dinostrato kvadratrisės savybes.

Priartėjimo metodas

Priartėjimo metodas skirtas srities ploto suradimui įbrėžiant į vidų seką daugiakampių, kurių plotas kaskart vis labiau artėja prie srities ploto. Jei seka sudaryta teisingai, tai n daugiakampio plotas nuo srities ploto skiriasi visai nežymiai. n didėjant vis labiau priartėjama prie srities ploto.

Ši idėja priskiriama Antifonui, nors neaišku, kaip giliai jis suvokė šį metodą. Teoriją pagrindė Eudoksas. (Archimedas jį naudojo pi reikšmės nustatymui – įbrėždamas į apskritimą vis daugiau kraštinių turinčius daugiakampius. Pirmąkart terminą („išsėmimo") 1647 m. savo knygoje panaudojo Gregorie de Saint-Vincent'as.

Naudojant šį metodą buvo gauti ir kiti rezultatai:

• tiesės ir parabolės ribojama sritis yra 4/3 dydžio lyginant trikampio, su tokiu pat pagrindu ir aukščiu;
• Elipsės plotas yra proporcingas stačiakampiui su šonais, lygiais elipsės ašims;
• Rutulio tūris yra 4 kartus didesnis už kūgį su tokio pat dydžio pagrindu ir aukščiu (lygiu spinduliui);
• Cilindro, kurio aukštis lygus diametrui, tūris yra 3/2 rutulio tūrio su tuo pačiu diametru;
• Srities, apribotos vienu spiralės apsisukimu ir linijos, yra 1/3 lyginant su skrituliu, kurio spindulys lygus linijos atkarpos ilgiui;
• ir t.t.

Priartėjimo metodas įrodomas pasinaudojant reductio ad absurdum principu. Jis buvo skaičiavimo metodų pirmtakas. Analitinės geometrijos ir integralinių skaičiavimų išvystymas 17-19 a. perdengė priartėjimo metodą ir jis dabar tiesiogiai nenaudojamas praktikoje.

Naujoji priartėjimo metodo forma leidžia paskaičiuoti bet kokios tolygios funkcijos integralą ir naudotina, kai nėra paprastų paskaičiavimo metodų:

© 2009. Visos teisės saugomos. Jokia teksto dalis negali būti panaudota be leidimo ir šaltinio nurodymo.

Parabolė
Žanas Furjė
Algebros istorija
Hiparchas iš Rodo
Dioklas ir jo cizoidė
Apolonijus iš Pergo
Hipatija – pirmoji matematikė
Parabolės lenktas likimas
Omaras Chajamas: ne vien Rubijatai
Iniciatyva: Matematikos keliu
Matematika Egipte ir Finikijoje
Didžiausias bendras daliklis
Matematika Egipte: Rindo papirusas ir kt.
Surasta trilijonas trikampių
Alef paslaptis: begalybės paieškos
Matematikai: Davidas Hilbertas
Graikų matematikai - filosofai
Algoritmų pirmeivis laimėjo Kyoto premiją
Australijos aborigenų matematikos samprata
J. Tate: Abelio premijos laureatas
8 alternatyvūs energijos šaltiniai
Nepaprastai suderinta Visatos sandara
21 a. mokslo idėjos ir švietimas
Matematikos filosofinės problemos
Tadžikai apie astronomiją
Santykis ir proporcija
Ar vasaros laikas taupo?
Pitagoro teorema
Meilės sinusoidė
Pirminiai dvyniai
Platonas
Vartiklis