Fraktalinė dimensija. |
|
Tarkime, turime aibę S. Pasirinkime bet kokį 
. Uždenkime aibę S atvirais rutuliais B(x0,r) taip, kad kikvieno rutulio spindulys r tenkintų 
. (Atviru rutuliu B(x0,r) vadinama aibė erdvės taškų, nutolusių nuo taško x0 atstumu, mažesniu už r. Vienmatėje erdvėje 'rutulys' yra atkarpa, plokštumoje skritulys, trimatėje erdvėje įprastas rutulys). Laikysime, kad mūsų aibė S yra aprėžta, ir kokį e bepasirinktume, yra minimalus aibę S dengiančių rutulių skaičius, kurį pažymėsime N(e).
Fraktalinės dimensijos apibrėžimas: Tegu S yra metrinės erdvės kompaktinis poaibis. Koks bebūtų , tegu N(e) mažiausias skaičius rutulių su spinduliais , kurių reikia aibei S uždengti. Tarkime egzistuoja baigtinis skaičius d, tenkinantis
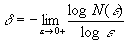Tuomet d vadinamas S fraktaline dimensija.
Pabandykime nustatyti ryšį tarp topologinės dimensijos ir fraktalinės dimensijos.
Imkime išmatuojamą kreivę, kurios ilgis L. šiuo atveju rutulys su spinduliu e uždengia apytiksliai 2e ilgio kreivės dalį. Taigi, L ilgio kreivei uždengti reikės apytiksliai 
rutulių. Todėl šiai kreivei 
,
t.y. fraktalinė dimensija sutampa su topologine.
Plokštumoje imkime sritį, kurios plotas A. Skritulys, kurio spindulys d, uždengs plotą, lygų pe2. Todėl visai sričiai uždengti reikės apytiksliai 
skritulių. Taigi tokios srities fraktalinė dimensija d=2, t.y. vėl sutampa su topologine dimensija.
Pavyzdžiai.
1. Pažiūrėsime, kokia yra Koch snaigės fraktalinė dimensija.
Prisiminkite, kaip konstruojama ši snaigė.
Imkime trikampį, kurio kraštinė lygi a. Po pirmojo žingsnio trikampio kraštinė virs laužte, sudaryta iš 4 dalių, kurių kiekvienos ilgis yra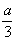 
. Po antrojo iš 42 dalių, kurių ilgis 
, po n tojo 4n dalių, kurių ilgis 
. Taigi, po n žingsnių snaigę sudarys 3*4n dalių, kurių ilgis . Visas Koch snaigės ilgis po n žingsnių bus 
. Kadangi Koch snaigė gaunama atlikus begalinį aprašytų žingsnių skaičių, o 
, kai 
, tai Koch snaigės ilgis begalinis.
Pasirinkime 
. Tuomet snaigei uždengti reikės apytiksliai 3*4n skritulių.
Taigi, Koch snaigės fraktalinė dimensija yra 1,26.
2. Nesunkiai įrodoma, kad Sierpinskio nėrinys yra nulinio ploto. Jei pasirinksime 
, kur R yra apie pradinį trikampį apibrėžto apskritimo spindulys. Tuomet Sierpinskio nėriniui uždengti reikės 3n skritulių. Sierpinskio nėrinio fraktalinę dimensiją gausime lygią 
.
Galima įrodyti, kad fraktalinė dimensija dF visada didesnė arba lygi topologinei dimensijai dT. Tačiau jei aibė S yra erdvėje Rn, tai fraktalinė dimensija dF(S) visada mažesnė arba lygi n.
Viso to išvada: fraktalinė dimensija yra topologinės dimensijos sąvokos praplėtimas, tam tkra interpretacija.
Minėtas fraktalinės dimensijos apibrėžimas turi keletą trūkumų, iš kurių pagrindinis tas, kad kai kuriems žinomiems kompaktiniams poaibiams pagal šį apibrėžimą fraktalinės dimensijos negalime nustatyti, nes riba
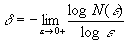neegzistuoja. Be to, kai kam atrodytų tinkamiau imti rutulius, kurių spinduliai griežtai lygūs e, o ne mažesni arba lygūs
e. Tačiau yra tokios kompaktinės aibės, kurioms skaičiujant fraktalinę dimensiją abiem atvejais gaunami ne tie patys rezultatai. Taigi, kai kurie fraktalinės dimensijos skaičiavimo aspektai vis dar neištirti.
Praktiniuose taikymuose dažnai paprastumo dėlei laikoma, kad gamtoje esančių fraktalų dimensijas galima apskaičiuoti "gražiai", t.y. skaičiuojant neiškyla minėtos problemos. Tai šiek tiek ironiška, nes "gamtos fraktalų geometrijos" pagrindinė idėja yra ta, kad gamtos negalima "gražiai" atvaizduoti klasikinės geometrijos objektais.
Taigi, ar tikrai gamtos fraktalai paklūsta dabartinei matematikai?
